I was working on Kokkos course that talks about data layout in memory.
I searched a bit about that and i find an interesting document that say : "The memory latency of random memory accesses due to pointer chasing through linked lists will not be reduced by the prefetch mechanisms."
It is very amazing the harware optimisation in modern processors , it is well explained in the full article:
This is true as far as it goes, but, in a performance-conscious Scheme or Lisp implementation (unlike in a naïve C program), the cons cells comprising a linked list are unlikely to be scattered at random locations in memory. Instead, the system will try to store the cons cells near each other, ideally in a contiguous block of memory. In some cases the allocator may be able to do this directly, but, even if not, a copying GC gives a second chance: after copying the skeleton of a cons cell, it can recur on the cdr, copying it to the next location in memory, before proceeding to recur on the car.
That’s not to say linked lists don’t have downsides, like the overhead of storing all of the cdrs. For many purposes, something like racket/treelist will be a more flexible choice. Still, the Lisp family of languages knows a lot about how to get the most from our historic, elegant data structure.
yes you're right, and i probably had still in mind our historic university course (slide 3):
http://jean.paul.roy.free.fr/PCPS/PF1/cours7-4p.pdf
which showed the cons cells scattered for a pedagogic goal, i suppose.
Even with arrays, threading is very tighted to hardware , it is a whole world , in Scheme and Racket i see often attempt to thread some applications, of course it depends of the level ,if we talk of system threads or CPU threads, or even GPUs ,it's could be completely different . Such a system as Kokkos in C++ try to solve this in a single common API. Relatively to C/C++ language, having a Scheme language that can generate C could be usefull.But it should be keep in mind that the language have to be able to deal with hardware constraints very closely. A simple example such as Trapezoidal Integration which is very classic show the difficulties when we get near the CPU in C and even assembly (see hardware instruction CMPXCHG compare-and-exchange in the document) ,see the solutions here:
and i do not even talk of caching problems.
Even with a Scheme ,there exist some as Gambit , that generate C ,i'm not sure we could get this parallelisation or threading to work.
You can certainly parallelize this example of trapezoidal/Riemann integration with Racket! Examples like this that are almost entirely floating-point number crunching have worked since the Racket BC days, but the better low-level thread-safety underlying Racket CS and the very recent language support for parallel threads in Racket 9.0 make an even broader class of problems work even better.
In my initial, not-carefully-tuned implementation below, I tried to follow closely the presentation in the OSU slides you linked, though I did not stoop to needlessly inserting set! when for/fold was at hand. The parallel version is supposed to resemble the reduction(+:sum) pragme. It follows the idea on slide 10 of each thread keeping a local, running sum. I did not try to implement a binary tree of reduction, as I suspect, on my 16-core machine, the communication overhead of additional complexity wouldn't pay off. Instead, I used flsum, which minimizes rounding error. (Recall that floating-point addition is not assosciative!)
If, instead, you wanted something similar to the #pragma omp atomic strategy, you could build something using functions like box-cas!. For the #pragma omp critical strategy, you probably need Racket 9.0's parallel threads, as futures can be interrupted at inconvenient times, but then you could use semaphores or "future semaphores" (or, unsafely, uninterruptible mode), with different trade-offs.
I would also note that generating #pragma omp parallel for default(none),shared(dx),reduction(+:sum) is not usually what is meant by compiling to the C programming language!
#lang racket
(module+ main
(printf ";; Sequential:\n")
(collect-garbage)
(collect-garbage)
(collect-garbage)
(time (sequential))
(printf ";; Parallel (~v cores):\n" (processor-count))
(collect-garbage)
(collect-garbage)
(collect-garbage)
(time (parallel)))
(require racket/flonum
math/flonum)
(define Function flsin)
#;
(define numSubdivisions 1000000000) ; -> 2.000000000001576
(define numSubdivisions 100000000) ; -> 1.9999999999999005
;;^ with (sequential), parallel result is 1.9999999999999791
(define A 0.0)
(define B pi)
(define dx
(fl/ (fl- B A)
(->fl (sub1 numSubdivisions))))
(define init-sum
(fl/ (fl+ (Function A) (Function B))
2.0))
(define (sequential)
(fl* (for/fold ([sum init-sum])
([i (in-range 1 (sub1 numSubdivisions))])
(define x
(fl+ A (fl* dx (->fl i))))
(define f
(Function x))
(fl+ sum f))
dx))
(define (parallel)
(define cpus
(processor-count))
(define jobs
(for/list ([job (in-inclusive-range 1 cpus)])
(future
(λ ()
(for/fold ([sum 0.0])
([i (in-range job (sub1 numSubdivisions) cpus)])
(define x
(fl+ A (fl* dx (->fl i))))
(define f
(Function x))
(fl+ sum f))))))
(fl* (flsum (cons init-sum
(map touch jobs)))
dx))
You take "à la lettre" (take literally) what i wrote. I was meaning,not only working, but for me a // schema should bring a strong enhancement, with openMP , on simple things, from my experience,if you have N processors , the speedup is often N*100%, i often got (N+1)*100% by faking the OPEN_MP_NUM_THREADS (not sure of the exactname) variable by forcing to get N+1 threads even if system hradware is only N CPUs because then you steal a bit the reserved CPUs for the Linux system to run (not to do on a multi-user cluster ! chance you're putting the system on knee)
What are the performance of your program?
But generally the performance is ,i admit, less than N*100% ,see this slide 46 for explanation of the Amdahl 's law.
This was just a fast answer. I will try to make tests as i'm working currently also with Kokkos tutorials for work but not with Scheme with clang compiler or Intel C compiler i'm just installed yesterday to be compatible with SYCL .
There was another thread about // in Racket ,where some test i already conducts lead only to 40% speed up on more than 10 CPus.
So i will not say it does not "work" but the performances are not good.In HPC no one will submit a job to a cluster in openMP,MPI over CPUs and GPUs over mutiple nodes to just get a 40% speedup!
I do not know where is the problem, is it with Scheme comparative with C only , or just the fact we have not in the Scheme community a system as OpenMP ? that can really get in the system a preemption over the CPUs as OpenMP do it?
So my idea (but i have no time for that now) would be to use a Scheme implementation that have strong relation with C language enougt to give to one C openMP or kokkos threaded a single Scheme routine compiled to C to launch it for test and get back the result to Scheme main program and see the performances.(many years i try something with Guile without getting any speed up perheaps because Guile have a C API but is not generating C code? )
To summarize, what i call a "working //" is something you get a very good speed up comparative with N cpus get at least or even better more than N/2 * 100% speedup for example having a 8 core system and getting 600 to 700% speedup means at least the threading work to split job take 200% - 400%of CPUs time and you gain 600% to 700% speedup. Otherwise it does not good to use so much electric energy and cpus time.
update:
i'm not saying threading in Scheme is bad. For example you can use if for threading web server multiple request to multiple web client . I already heard of that working well.I'm was just talking about threading in Scheme for HPC which is something very different.
That article is correct, but I think you are misunderstanding it, confusing latency with throughput.
Even when it works, prefetch can not reduce latency of memory fetches - they are what they are and depend on whether the data is in memory or somewhere in the cache hierarchy. The point of hardware prefetch is to increase processing throughput and reduce end-to-end time by issuing data requests earlier than might be apparent from the code.
There's a saying in hardware design: "it takes 3 cycles to multiply two numbers, but 300+ cycles to bring the numbers to the multiplier". [Yes, some CPUs can multiply in 3 cycles, and the average fetch-from-memory latency is 300 cycles. Take a browse in comp.arch on Usenet if you want to discuss things with actual CPU architects.]
Modern prefetch mechanisms can recognize moderately complex fetch patterns and certainly can work with various list structures. But if the processing at each list node takes less time than fetch of the next node, then prefetch will not buy you much.
WRT arrays: fetch (or prefetch) is done by cache line, which for numeric code typically brings in more than one array element with each fetch. Typical commodity CPU cache lines hold 4 to 8 double precision values - server class CPUs even more.
You can deliberately prefetch the next by referencing it in your code before working on the current . A lot of high performance code does this - the trick is to convince the compiler not to remove the reference as dead code. Modern C compilers allow to query cache characteristics to tune the code as best as possible. Scheme / Racket does not.
Hope this ... doesn't confuse more.
George
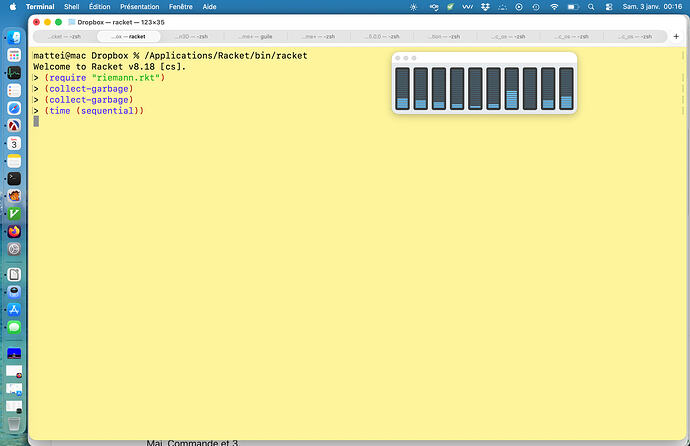
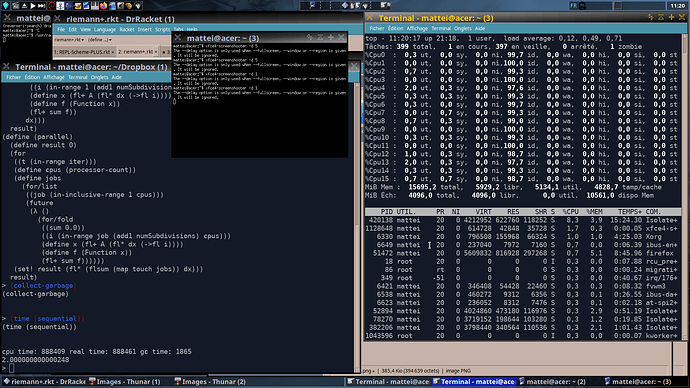
Not so bad with Racket/future in command line interface, compared to C++/Kokkos (OpenMP):
one can see in sequential that 10 cores are lightly used.
in // the 10 cores are heavily loaded.
and the result is faster:
factor >2 but with 10 cores.
Comparing with C++/Kokkos on 1 core:
And with 10 cores,again coresare loaded:
and the speed:
factor of 4 but still with 10 cores.
and approx 3.5times faster than Racket
The code used:
#lang racket
(module+ main
(printf ";; Sequential:\n")
(collect-garbage)
(collect-garbage)
(collect-garbage)
(time (sequential))
(printf ";; Parallel (~v cores):\n" (processor-count))
(collect-garbage)
(collect-garbage)
(collect-garbage)
(time (parallel)))
(provide sequential
parallel)
(require racket/flonum
math/flonum)
(define Function flsin)
#;
(define numSubdivisions 1000000000) ; -> 2.000000000001576
(define numSubdivisions 100000000) ; -> 1.9999999999999005
;;^ with (sequential), parallel result is 1.9999999999999791
(define A 0.0)
(define B pi)
#;(define dx
(fl/ (fl- B A)
(->fl (sub1 numSubdivisions))))
(define dx
(fl/ (fl- B A)
(->fl numSubdivisions)))
#;(define init-sum
(fl/ (fl+ (Function A) (Function B))
2.0))
(define iter 500)
(define (sequential)
(define result 0)
(for ((t (in-range iter)))
(set! result (fl* (for/fold ([sum 0.0 #;init-sum])
([i (in-range 1 (add1 #;sub1 numSubdivisions))])
(define x
(fl+ A (fl* dx (->fl i))))
(define f
(Function x))
(fl+ sum f))
dx))
)
result
)
(define (parallel)
(define result 0)
(for ((t (in-range iter)))
(define cpus
(processor-count))
(define jobs
(for/list ([job (in-inclusive-range 1 cpus)])
(future
(λ ()
(for/fold ([sum 0.0])
([i (in-range job (add1 #;sub1 numSubdivisions) cpus)])
(define x
(fl+ A (fl* dx (->fl i)))) ; A + dx * i
(define f
(Function x))
(fl+ sum f))))))
(set! result (fl* (flsum ;(cons init-sum
(map touch jobs));)
dx))
)
result
)
C++/Kokkos :
#include <limits>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <Kokkos_Core.hpp>
int main( int argc, char* argv[] )
{
const int N = 100000000; // nombre de sous-intervalles
const double a = 0.0;
const double b = M_PI;
const double dx = (b - a) / N;
int nrepeat = 30; // number of repeats of the test
// Read command line arguments.
for ( int i = 0; i < argc; i++ ) {
if ( strcmp( argv[ i ], "-nrepeat" ) == 0 ) {
nrepeat = atoi( argv[ ++i ] );
}
else if ( ( strcmp( argv[ i ], "-h" ) == 0 ) || ( strcmp( argv[ i ], "-help" ) == 0 ) ) {
printf( " riemann Options:\n" );
printf( " -nrepeat <int>: number of repetitions (default: 100)\n" );
printf( " -help (-h): print this message\n\n" );
exit( 1 );
}
}
Kokkos::initialize( argc, argv );
{
// Timer products.
Kokkos::Timer timer;
for ( int repeat = 0; repeat < nrepeat; repeat++ ) {
// Application: riemann integral
double integral = 0.0;
Kokkos::parallel_reduce( "RiemannIntegral",
N,
KOKKOS_LAMBDA ( int i, double &local_sum ) {
double x = a + i * dx;
local_sum += Kokkos::sin(x); //std::sin(x);
},
integral );
integral *= dx;
// Output result.
if ( repeat == ( nrepeat - 1 ) ) {
printf( " Computed result for Integral is %lf\n", integral );
}
}
double time = timer.seconds();
// Print results (problem size, time and bandwidth in GB/s).
printf( " N( %d ) nrepeat ( %d ) time( %g s ) \n",
N, nrepeat, time );
}
Kokkos::finalize();
return 0;
}
If i test it on may Linux box:
My Linux Intel7 box seems really slower than Apple M4 even with the 16 cores,and only in // it can save the game a little:
with a factor speedup of 6 with the 16 cores , this is not really what i expected from //.
Let see with C++/Kokkos if it performs better? :
The serial run on only one cpu give this time:
About all the articles about computer architecture we can find on the net, i admit it is a bit confusing.I think there is a gap between the guys that do the CPU architecture, and the ones who wrote compilers, and at last the programmers. A lot of times I can personnally hardly find what concretely i can do of all those informations.
"But building programmable hardware that only 5 people in the world can program ain’t a winning strategy, I’d humbly suggest." (from linked article)
